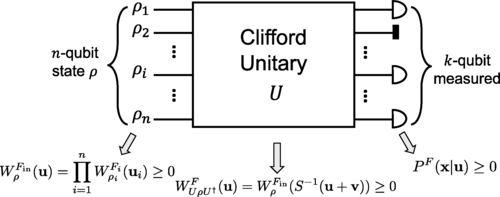
The Wigner function formalism has played a crucial role in quantifying the nonclassical aspects of quantum states and their classical simulate-ability. Nevertheless, its application in qubit systems faces limitations due to negativity induced by Clifford gates. In this work, we propose a novel classical simulation method for qubit Clifford circuits based on the framed Wigner function, an extended form of the Wigner function with an additional phase degree of freedom. In our framework, Clifford gates do not induce negativity by switching to a suitable frame; thereby, a wide class of non-stabilizer states can be represented positively. By leveraging this technique, we show that some marginal outcomes of Clifford circuits with non-stabilizer state inputs can be efficiently sampled at polynomial time and memory costs. We develop a graph-theoretical approach to identify classically simulate-ability marginal outcomes and apply it to log-depth random Clifford circuits. We also present the outcome probability estimation scheme using the framed Wigner function and discuss its precision. Our approach opens new avenues for utilizing quasi-probabilities to explore classically simulate-ability quantum circuits.